FROM CLAMP TO CRAMP OF LOGIC: EXPLICATING THE CHAGRINS OF SYMBOLIC LOGIC.
Anacletus Ogbunkwu
Department of Philosophy,
Godfrey Okoye University, Enugu.
This email address is being protected from spambots. You need JavaScript enabled to view it..
Abstract
Though there is a general fanfare exalting symbolism as a basic appurtenance of logic and characteristically fundamental to logic; this paper argues that symbolism rather cramps and leads logic to a stampede. Using the methods of hermeneutics and logical syllogism, this paper reviews the claims of symbolism as a clamp and fundamental appurtenance of logic. The paper critically presents synopsis on understanding logic, symbolic logic and the tenets of arguments surrounding symbolic logic. On appraisal, it is revealed that logic is an essential need to humanity and the quintessence of humanness but symbolic logic denies humanity this essential possession since it relativizes logic only to the initiates in symbolic logic. However, this paper shows that even among the initiates, symbolic logic houses lots of inconsistencies, and ambiguities as different symbols have been used by different logicians and systems of logic in their claims that symbolic logic is needful for precision and elegance. Hence if philosophy is only possible as logic following the claims of some philosophers and symbolism is the fundamental appurtenance of logic, the implication is that it becomes an impossibility for humanity everywhere to access logic and a difficulty for logic to fulfil its objectives. It therefore holds that the fundamental objectives of logic towards sound reasoning and argumentation are put on edge by symbolic logic and this is what the paper refers as the chagrins of symbolic logic.
Key words: logic, symbolism, operators, chagrins, reason,
Introduction
There is a common assumption that the apogee of logicism is achieved in symbolic logic while symbolic logic implies the science and method of representing logical expressions through the use of symbols and variables, rather than in ordinary language. Hence symbolism is a basic appurtenance of logic and characteristically fundamental to logic towards facilitating logical ability[1]. It is from this perspective that this paper refers to symbolic logic as a clamp to logic that is, a strengthening brace to logic.
Nevertheless, this paper bears much concern on the inescapable reality before us that symbolic logic mounts unbearable and devastating effects on the objectives of logic leading to the cramp of logic. Thus these devastating effects inhibit and impede the actualization of the ends of logic which is the quest for correct reasoning and sound argumentation. In symbolic logic, these objectives are rather traded for precision and elegance.
Hence the task before us is the responsibility of explicating these inhibitions and impediments which this paper refers to the chagrins of symbolic logic. Undoubtedly, symbolism imposes heavy burden on logic in the process of transcription from ordinary language to symbolic language. Unfortunately, during this process, logic is greeted with ambiguity, inconsistency and lost of focus.
Our thesis in this essay is; in spite of the benefits of symbolic logic, its challenging effects are burdensome minding the aims of logic. Hence this is a wakeup call on all logicians towards finding ways to mitigate these afore mentioned challenges of symbolic logic.
Understanding Logic.
Logic is primarily an epistemological tool. Etymologically, logic is the anglicized form of the Greek word, logikḗ {(λογική) meaning: "possessed of reason, intellectual, dialectical, argumentative"} which has its root derived from logos {(λόγος) meaning: "word, discourse, rule, thought, idea, argument, account, reason, or principle"}.[2] The New Testament Gospel recognizes logos as synonymous to God as used in the Gospel of John[3]. This etymological derivations put together appropriately defines logic as the principles of correct reasoning. It is the method whoever wants to reason or argue correctly ought to follow but it is not within the scope of logic to lure people into following these principles. Hence Frege states that it is the task of logic to discover the laws of truth.[4] Uduma adds, ‘these laws of thought must be laws of correct reasoning’[5] such that appraisal of reasoning becomes the subject matter of logic.
According to Hegel, logic is the form taken by the science of thinking in general[6].The subject matter of logic is argument such that logic is indispensable to human existence. Quoting Spencer, Uduma maintained that while birds can fly, only human beings can argue. Hence argument for him, is the affirmation of our being. Like Spencer, he affirmed that human life is directed by argumentation[7]. It is the disposition to fundamental ordered action. Thus it is the necessary condition for order and intelligibility in reality. Therefore, we boldly emphasize here that, human thought process, actions and inactions are bye products of human reasoned private arguments and judgements. Logic is indeed needful in life and existence. [8]
Therefore, it is obvious that human life becomes wild and strange when one loses this essential and distinguishing element of being human. Even the Christians recognize that in creation, God made man different from animals just by the gift of reason. While he gave mere instinct to the lower animals, he gave reason to man. Little wonder when one acts without reason, he can be said to be inhuman or at best described as animal. Thus in such situation, one may be said to have lost the quintessence of humanness. Uduigwomen sees logic as the science which “helps us to weigh the merits and demerits of an action or decision before we venture into it, and hence enables us to take a balanced action or decision. Instead of engaging in endless controversies of trivial matters, it enables us to sift the evidence before us”[9].
Logic can be said to be the pattern of thought found in everyday discourse of a people. It is in this sense that one can conveniently talk about logic to have a cultural background. We agree with Momoh as follows:
in everyday usage of natural language we talk of a person as being logical if he is reasonable, sensible and intelligent; if he can unemotionally and critically evaluate evidence or a situation; if he can avoid contradiction, inconsistency and incoherence, or if he can hold a point of view argue for and from it, summon counter-examples and answer objections[10].
Logic is typically an element of culture. Whatever is judged, reasoned, thought or argued is according to the categories of the judging, thinking or reasoning mind as given by the environment. This mind is a product of a particular culture. Hence people’s background and temperaments influence their logic and thought process. Just as the Westerners have their ability to conduct their daily affairs following the givens of their environment, the Africans too have the same ability as regulated by their immediate experience and world views. This implies that the westerners, as well as the Africans are logical but their logic(s) is/are products of their varied experiences.
Logic can be either formal or informal. The discussion on logic so far bothers on informal logic whereby logic is interested in correct reasoning, right thinking and acts as agent of meaningful living. It is the branch of logic whose task it is to develop non-formal standards, criteria, procedures for the analysis, interpretation, evaluation, criticism and construction of argumentation in everyday discourse.[11] This form of logic is typical of African logic.
On the other hand, formal logic is concerned with specialties and specialization in logic. It can also be referred as Aristotelian, mathematical, artificial or critical logic. This is typical of western logic. The historical roots of logic go back to the work of Aristotle (384–322 BCE), whose syllogism was the standard account of the validity of arguments. The ancient times till 19th century witnessed a wide acceptance of Aristotelian logic. Logic earlier this modern period was championed by the Aristotelian method as contained in the Organon. Philosophers and commentators after Aristotle grouped Aristotle’s six logical treatises into a manual they called the Organon which is the Greek translation for “tool”. The Organon comprises the following works of Aristotle: the Categories, On Interpretation, Prior Analytics, Posterior Analytics, the Topics, and On Sophistical Refutations. These works give us a good understanding of Aristotelian logic especially as it concerns; structure/rules of arguments and syllogisms, logical structure of propositions, difference between induction and deduction, the nature of scientific knowledge, basic fallacies, debate techniques, to mention but a few[12].
The basis of Aristotelian formal logic is anchored on his three fundamental laws of reason, namely; the law of Identity, the law of Contradiction and the law of Excluded Middle. The first law states that a thing is always equal to or identical with itself. The second law states that a thing cannot be unequal or different from itself. Also, the third law continues the former two laws; it states that if a thing is equal to itself, it cannot be unequal or different from itself[13]. For example; if ‘y’ equals ‘z’, it cannot equal ‘non y’. Regarding the three laws of thought, we think that Aristotle has made a giant stride in formal logic. Formal logic is chiefly concerned with the processes of thinking and reasoning as well as the symbolic expression of such process in verbal or written form.[14]
Understanding Symbolic Logic
Symbolic logic is the science and method of representing logical expressions through the use of symbols and variables, rather than in ordinary language. This has the benefit of removing the ambiguity that normally accompanies ordinary languages in order to give way to easier operation of reason[15]. Symbolic logic can be referred as artificial language. This is the form of logic which places precedence to logical forms than ordinary statements. There are many systems of symbolic logic, such as classical propositional logic, first-order logic and modal logic. Each may have separate symbols, or exclude the use of certain symbols.[16]
According to the analysis of C. I. Lewis, the three characteristics of symbolic logic are:
(1) The use of symbols to stand for concepts, rather than ordinary language
(2) The use of the deductive method.
(3) The use of variables.[17]
For the reason of the difficulties experienced in the use of natural language in logic, symbolic logic claims to offer a better way forward. Hence Copi stated as follows;
the words used may be vague or equivocal, the construction of the argument may be ambiguous, metaphors or idioms may confuse or mislead, emotional appeals may distract ... to avoid these difficulties, and thus move directly to the logical heart of an argument, logicians construct an artificial symbolic language, free of linguistic defects. With symbolic language we can formulate an argument with precision[18].
According to Alfred Whitehead, symbols facilitate our logical ability[19]. Quite unlike Aristotelian logic that had syllogism as its end in logical activity, modern logic has logical connectives accounting for the internal structure of propositions and arguments.[20] Hence according to Uduma, ‘the development of symbolic logic is undoubtedly the most significant in the two thousand years of logic, and arguably, one of the most important events in human intellectual history.[21]
For Uduma, “symbolic reasoning is reasoning in a large scale with instruments appropriate to such wholesale undertakings”[22]. Hence he argued that the employment of special symbols in logic is both for practical convenience and logical necessity[23].
Gorge Boole is said to be the father of symbolic logic. The discipline of symbolic logic exploded in complexity as techniques of algebra were applied to issues of logic in the work of George Boole (1815–1864), Augustus de Morgan (1806–1871), Charles Sanders Peirce (1839–1914), and Ernst Schroder (1841–1902) in the nineteenth century[24]. They applied the techniques of mathematics to represent propositions in arguments hence treating the validity of arguments like equations in applied mathematics[25].
Furthermore, connections between mathematics and logic developed into the twentieth century with the work of Gottlob Frege (1848–1925) and Bertrand Russell (1872–1970), who used techniques in logic to study mathematics. Their goals were to use the newfound precision in logical vocabulary to give detailed accounts of the structure of mathematical reasoning, in such a way as to clarify the definitions that are used, and to make fully explicit the commitments of mathematical reasoning. This is manifest in the Principia Mathematica (1912) of Russell and Alfred North Whitehead.
Logical Symbols
In logic, a set of symbols is commonly used to express logical representation.[26] The following table presents several logical symbols, their name and meaning, and some relevant notes. It should be noted that different symbols have been used by different logicians and systems of logic. Nevertheless, for the sake of clarity, the column on the left hand side shows the symbols while the middle column shows the meanings or names of the symbols and the right hand side of the column shows further notes on the symbols with alternative symbols or other commonly-used symbols[27].
|
Symbol |
Meaning |
Notes |
|
Operators (Connectives) |
||
|
¬ |
negation (NOT) |
The tilde ( ˜ ) is used in alternative. |
|
∧ |
conjunction (AND) |
The ampersand ( & ) or dot ( · ) are also used in alternative. |
|
∨ |
disjunction (OR) |
This is the inclusive disjunction, equivalent to and/or/or both in English. |
|
⊕
|
(XOR)
|
⊕ means that only one of the connected propositions is true, equivalent to either…or but not both. Sometimes ⊻ is used. |
|
| |
(NAND) |
Means “not both”. Sometimes written as ‘↑’ |
|
↓ |
joint denial (NOR) |
Means “neither/nor”. |
|
→ |
conditional (if/then) |
Many logicians use the symbol ⊃ instead. This is also known as material implication. |
|
↔
|
biconditional (iff) (Triple bar) |
Means “if and only if” ≡. This is also used for material equivalence. |
|
Quantifiers |
||
|
∀ |
Means “all or for all”, so ∀xPx means that Px is true for every x. |
|
|
∃
|
|
Means “there exists or indicates that one or two or more unspecified individuals have property”. Hence ∃xPx means that Px is true for at least one x. |
|
Relations |
||
|
⊨ |
α ⊨ β means that β follows from α |
|
|
≡ |
Also ⇔. Equivalence is two-way implication, so α ≡ β means α β and β α. |
|
|
⊢ |
Shows provable inference. α β means that from α we can prove that β. |
|
|
∴ |
Used to signify the conclusion of an argument. Usually taken to mean implication, but often used to present arguments in which the premises do not deductively imply the conclusion. |
|
|
⊩ |
A relationship between possible worlds and sentences in modal logic. |
|
|
Truth-Values |
||
|
⊤ |
May be used to replace any tautologous (always true) formula. |
|
|
⊥ |
May be used to replace any contradictory (always false) formula. Sometimes “F” is used. |
|
|
Parentheses |
||
|
( ) |
Used to group expressions to show precedence of operations. Square brackets [ ] are sometimes used to clarify groupings. |
|
|
Set Theory |
||
|
∈ |
Denotes membership in a set. If a ∈ Γ, then a is a member (or an element) of set Γ. |
|
|
∪ |
Used to join sets. If S and T are sets of formula, S ∪ T is a set containing all members of both. |
|
|
∩ |
The overlap between sets. If S and T are sets of formula, S ∩ T is a set containing those elemenets that are members of both. |
|
|
⊆ |
A subset is a set containing some or all elements of another set. |
|
|
⊂ |
A proper subset contains some, but not all, elements of another set. |
|
|
= |
Two sets are equal if they contain exactly the same elements. |
|
|
∁ |
∁(S) is the set of all things that are not in the set S. Sometimes written as C(S), S or SC. |
|
|
- |
T - S is the set of all elements in T that are not also in S. Sometimes written as T \ S. |
|
|
∅ |
The set containing no elements. |
|
|
Modalities |
||
|
□ |
Used only in modal logic systems. Sometimes expressed as [] where the symbol is unavailable. |
|
|
◊ |
Used only in modal logic systems. Sometimes expressed as <> where the symbol is unavailable. |
|
Propositions, Variables and Non-Logical Symbols
Propositions, variables and non-logical symbols which serve the system of symbolic logic are presented below. For clarity sake; these propositions variables and non-logical symbols are presented with their corresponding names and meanings as below:
|
Symbol |
Meaning |
Notes |
|
A, B, C … Z |
Uppercase Roman letters signify individual propositions. For example, P may symbolize the proposition “Pat is ridiculous”. X, P and Q are traditionally used in most examples. |
|
|
α, β, γ … ω |
Lowercase Greek letters signify formulae, which may be themselves a proposition (P), a formula (P ∧ Q) or several connected formulae (φ ∧ ρ). |
|
|
x, y, z |
Lowercase Roman letters towards the end of the alphabet are used to signify variables. In logical systems, these are usually coupled with a quantifier, ∀ or ∃, in order to signify some or all of some unspecified subject or object. By convention, these begin with x, but any other letter may be used if needed, so long as they are defined as a variable by a quantifier. |
|
|
a, b, c, … z |
Lowercase Roman letters, when not assigned by a quantifier, signifiy a constant, usually a proper noun. For instance, the letter “j” may be used to signify “Jerry”. Constants are given a meaning before they are used in logical expressions. |
|
|
Ax, Bx … Zx |
Uppercase Roman letters appear again to indicate predicate relationships between variables and/or constants, coupled with one or more variable places which may be filled by variables or constants. For instance, we may definite the relation “x is green” as Gx, and “x likes y” as Lxy. To differentiate them from propositions, they are often presented in italics, so while P may be a proposition, Px is a predicate relation for x. Predicate symbols are non-logical — they describe relations but have neither operational function nor truth value in themselves. |
|
|
Γ, Δ, … Ω |
Uppercase Greek letters are used, by convention, to refer to sets of formulae. Γ is usually used to represent the first site, since it is the first that does not look like Roman letters. (For instance, the uppercase Alpha (Α) looks identical to the Roman letter “A”) |
|
|
Γ, Δ, … Ω |
In modal logic, uppercase greek letters are also used to represent possible worlds. Alternatively, an uppercase W with a subscript numeral is sometimes used, representing worlds as W0, W1, and so on. |
|
|
{ } |
Curly brackets are generally used when detailing the contents of a set, such as a set of formulae, or a set of possible worlds in modal logic. For instance, Γ = { α, β, γ, δ } |
Truth Table
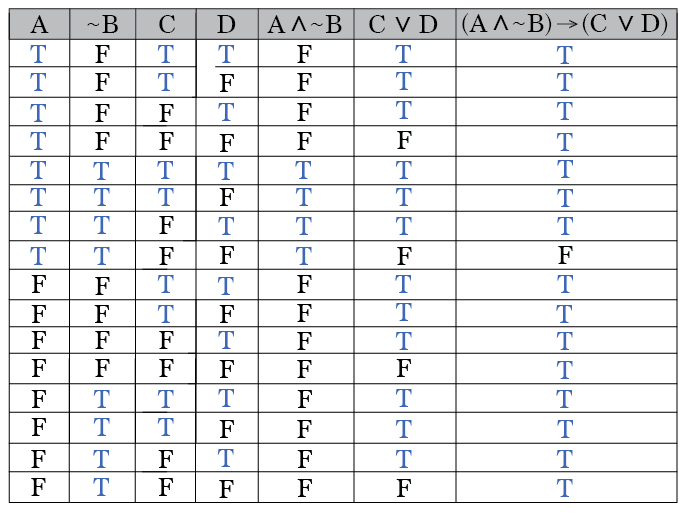
Explicating the Chagrins of Symbolic Logic
Logic has been defined as the principle of correct reasoning and a necessary condition for order and intelligibility in reality and as such very needful in life and existence. [28] While other animals have mere instinct, man has reason so much so that when one acts without reason, he can be said to be inhuman and to have lost the quintessence of humanness.
In the same vein, symbolic logic is a branch of logic and the method of representing logical expressions through the use of symbols and variables, rather than in ordinary language. This form of logic claims to remove the ambiguity that normally accompanies ordinary languages in order to give way to easier operation of reason[29]. Similarly, this form of logic facilitates our logical ability[30]. For the reason of the difficulties experienced in the use of natural language in logic, symbolic logic claims to offer a better way forward towards formulating arguments with precision[31]. Hence Uduma stated that the employment of special symbols in logic is both for practical convenience and logical necessity[32].
In spite of the above mentioned support and clamp which symbolism offers to logic, this paper asserts that symbolic logic mounts some degree of disquietude and uneasiness thereby making logic to stray away from its primary purpose on correct reasoning and sound argumentation to precision and practical convenience. Hence we choose to refer to this form of disquietude and uneasiness as the chagrins of symbolic logic.
One of the major chagrins of symbolic logic is that symbolism imposes heavy burden on logic. This heavy burden is a product of translating deductive arguments to symbolic logic. Hence an argument already existing or whose conclusion has been drawn would begin a fresh process of transcription to symbolism. Man does not necessarily think in those symbols but translate already established argument into symbolism just for precision and elegance.
In the same vein, this attempt on transcription of arguments to symbolism sometimes leads to the lost of meaning and ambiguity. This already challenges the objective which symbolic logic set to achieve; that is, avoiding ambiguity inherent in ordinary language. Hence here symbolic logic falls a victim of its own charge. Though a set of symbols is commonly used to express logical representation[33], sometimes different symbols have been used by different logicians and systems of logic thereby making argumentation uneasy, inconsistent and ambiguous.
Momoh is right to claim that the limitation imposed on logic as dictated by the formal language logic paradigm is quite disquieting[34]. Regarding informal logic, Uduma emphatically declared as follows:
the point here is that all we need can be conducted in a natural language. Symbolism is just for elegance and precision. Clarity of expression, avoidance of ambiguities and contradictions which are central to logic can be effectively conducted in natural languages[35].
Uduma makes the point clear enough here that symbolic logic is just for elegance and precision which are not really the aim of logic rather correct reasoning and good argumentation. Nevertheless, we make bold to query the formal language logicians as follows;
- Does everyone have the knowledge of symbolic logic? A no answer here implies that only the privileged initiates in symbolism who have knowledge of symbolic logic can think logically, communicate and act with logic. This cannot be true!
- Do the initiate symbolic logicians think with formal language or symbolic logic before they act? Do they run their daily affairs with symbolic logic? Definitely the answer ought to be in the negative! Natural language logic suffices here.
- Was the entire world non critical or non reflective before the advent of Aristotelian logic and the symbolic logic? Definitely the answer is in the negative. Even before Aristotle himself, man was critical and reflective. This was why he claimed that the distinguishing characteristic of man is his rationality.
It is a bogus assumption and futile expectations to presume that my grandmother in the village cannot think or act logically because she is not a symbolic logician. I sit down here to imagine the confusion in her head when I go home and instead of telling her:
mama this drug makes people powerful and beautiful
you have taken the drug
therefore you are powerful and beautiful’
I tell her
P ∧ B
Or I tell her P . B
Here it is obvious that symbolic logic is not for everyone but for the initiates in symbolism. Hence here, this paper is not denying the importance of symbolic logic but only proves that it is relative only to the initiates in symbolism.
Conclusion
The paper has made dogged effort towards giving a good understanding of logic, symbolic logic and the tenets of arguments surrounding symbolic logic as a necessity in logic. The paper has emphasized logic as the principle of correct reasoning. Also, symbolic logic has been defined as the science and method of representing logical expressions through the use of symbols and variables, rather than in ordinary language.
According to Uduma, ‘the development of symbolic logic is undoubtedly the most significant in the two thousand years of logic, and arguably, one of the most important events in human intellectual history.[36] There is a general claim that the apogee and epicentre of logic lies in symbolic logic being one of the most recent developments in the field of logic.
Nevertheless, our logic in this paper is that symbolism has not completely solved the problems it claims to solve in the field of logic. It rather creates more problems to logic than it solves. Symbolic logic claimes to be fundamental to logic but warrants lost of focus on the objectives of logic from correct reasoning and sound argumentation to precision and elegance.
If the aims of logic as clarity of expression, avoidance of ambiguities and contradictions can be effectively conducted in natural languages, symbolic logic can therefore be said to be second hand logic. Thus the work of logic is already achieved before the application or translation to symbolism. More so even when this translation or transcription to symbolic logic is made, logic in most cases becomes ambiguous and vague following the fact that different symbols have different meanings and applications.
If logic is the process of correct reasoning, it is not proven anywhere that anyone had ever reasoned with symbolic logic. We rather reason in ordinary language then re-write our reason to symbolism. Similarly, if symbolism is a necessary condition to logic, the non initiates in symbolism would be illogical in reasoning. This is not the case because those who do not know the formal or artificial language of logic still exercise good principles of correct reasoning and sound argumentation. Hence we claim that in spite of the benefits of symbolic logic, its challenging effects are burdensome minding the aims of logic.
End Notes
[1] Alfred North Whitehead, An Introduction to Mathematics, (New York: H. Holt and Company publishers, 1861), p.1911.
[2] Liddell & Scott, “Logic” http://www.iep.utm.edu/aris-log/ accessed on 20/4/17
[3] John 1.1ff
[4] Liddell & Scott, “Logic” http://www.iep.utm.edu/aris-log/ accessed on 20/4/17
[5] Uduma Orji Uduma, “Explicating the Formal Nature of Logic”, in The Nigerian Journal of Philosophy, Vol., 23, No. 2, (Lagos: University Press, 2009). P. 127.
[6] Georg Wilhelm Friedrich Hegel; The Science of Logic, (Cambridge: University Press, 2010), p. 24
[7] Uduma O. Uduma, “Can There Be An African Logic”? in Uduigwomen A., From Footmarks to Landmarks on African Philosophy, 2nd ed., (Lagos: Obaroh & Ogbinaka Pub., Ltd, 1997), p. 273
[8] Copi, Irving. Introduction to Logic. 6th (ed). (New York: Macmillan, 1982). P.vi
[9] Uduigwomen, A.F., How to Think: An Introductory Text on Logic, Argumentation and Evidence. (Aba: A.A.U. Vitalis Books Co., 2003), p.19
[10] Momoh, C.S. (ed) The Substance of African Philosophy. (Auchi: African Philosophy Projects Publications, 1989), P.174
[11] Ralph H. Johnson, The Rise of Informal Logic, (London: University Press, 2014), p. 13.
[12]James Fieser, Internet Encyclopadia of Philosophy, http://www.iep.utm.edu/eds/ accessed on May 15, 2017.
[13] John Venn, Symbolic Logic, (Cambridge: Cambridge University Press, 1990), p.43
[14] Corpi, I.M. and Cohen, C. Introduction to Logic. (USA: Macmillan Publishers, 1994), p.23.
[15] http://study.com/academy/lesson/symbolic-logic-definition-examples.html accessed on 01/12/2017
[16] Franklin, C. L. (1889). “On some characteristics of symbolic logic”. In The American Journal of Psychology, 2(4), 543-567.
[17] https://proofwiki.org/wiki/Definition:Symbolic_Logic, 05/11/2017
[18] Irving Copi and Carl Cohen, Introduction to Logic, 11th edi., (Singapore: Pearson Education, 2002), p. 299
[19] Alfred North Whitehead, An Introduction to Mathematics, 1911,
[20] Irving Copi and Carl Cohen, Introduction to Logic, 11th edi., (Singapore: Pearson Education, 2002), p.300
[21] Uduma Oji Uduma, Introduction to Logic and the Fundamentals of Formal Reasoning, 2nd ed., Accra Ghana: Africa Analytica Publishers, 2015, 237.
[22] Uduma Oji Uduma, Introduction to Logic and the Fundamentals of Formal Reasoning, 2nd ed., Accra Ghana: Africa Analytica Publishers, 2015, 243.
[23] Uduma Oji Uduma, Introduction to Logic and the Fundamentals of Formal Reasoning, 2nd ed., Accra Ghana: Africa Analytica Publishers, 2015, p.243.
[24] Ewald, William, ed. 1996. From Kant to Hilbert: A Source Book in the Foundations of Mathematics. (Oxford: Oxford University Press, 1996), p. 132.
[25] Alfred North Whitehead, An Introduction to Mathematics, 1911
[26] https://en.wikipedia.org/wiki/List_of_logic_symbols, 09/01/2018
[27] http://www.philosophy-index.com/logic/symbolic/, 09/01/2018
[28] Copi, Irving. Introduction to Logic. 6th (ed). (New York: Macmillan, 1982). P.vi
[29] http://study.com/academy/lesson/symbolic-logic-definition-examples.html, 09/01/2018
[30] Alfred North Whitehead, An Introduction to Mathematics, 1911,
[31] Irving Copi and Carl Cohen, Introduction to Logic, 11th edi., Singapore: Pearson Education, 2002, p. 299
[32] Uduma Oji Uduma, Introduction to Logic and the Fundamentals of Formal Reasoning, 2nd ed., Accra Ghana: Africa Analytica Publishers, 2015, p.243.
[33] https://en.wikipedia.org/wiki/List_of_logic_symbols, 09/01/2018
[34] C. S. Momo, “The Logic Question in African Philosophy” in C. S. Momoh ed., The Substance of African Philosophy, (Auchi: African Philosophy Projects Publications), p. 23 quoted in Uduma, O. Uduma, “Logic As An Element of Culture: In Defense of Logic in African Traditional Thought”, P. 187.
[35] Uduma, O. Uduma, “Logic As An Element of Culture: In Defense of Logic in African Traditional Thought”, p.184
[36] Uduma Oji Uduma, Introduction to Logic and the Fundamentals of Formal Reasoning, 2nd ed., (Accra Ghana: Africa Analytica Publishers, 2015), p. 237.
